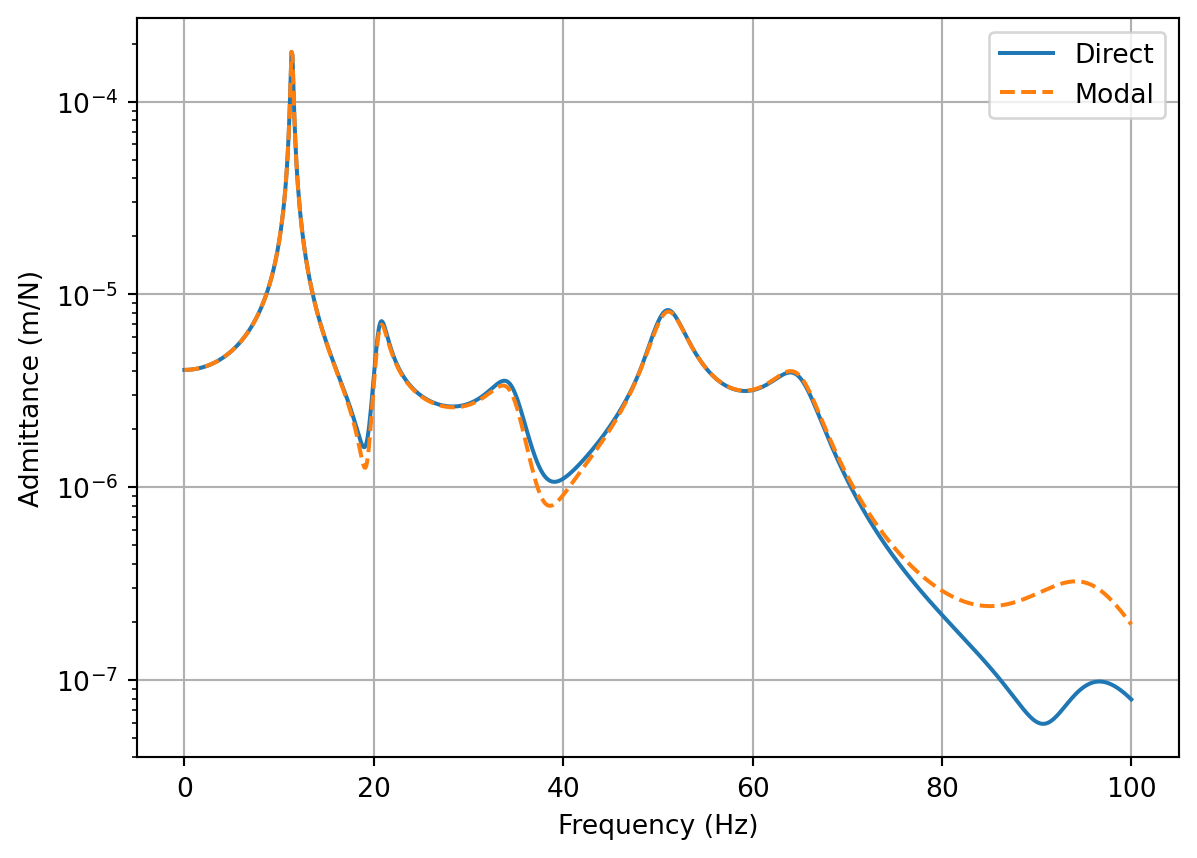
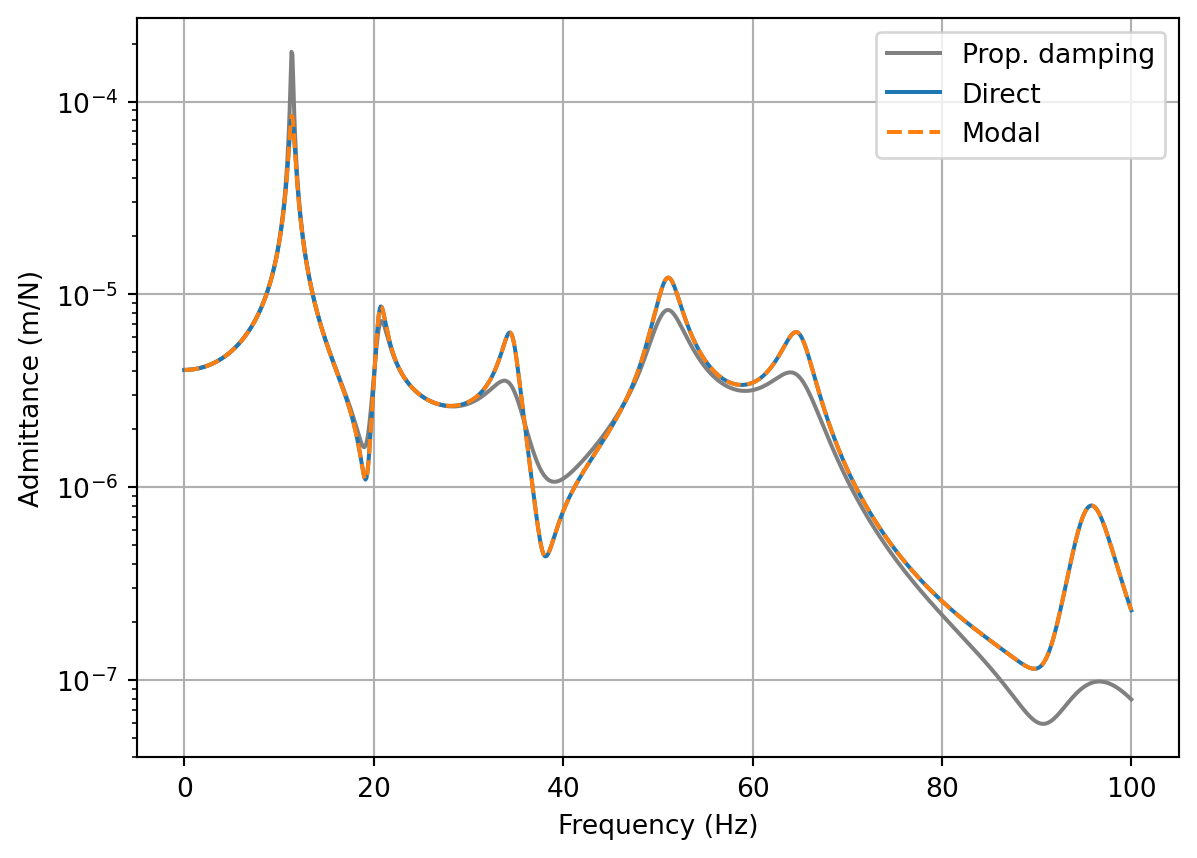
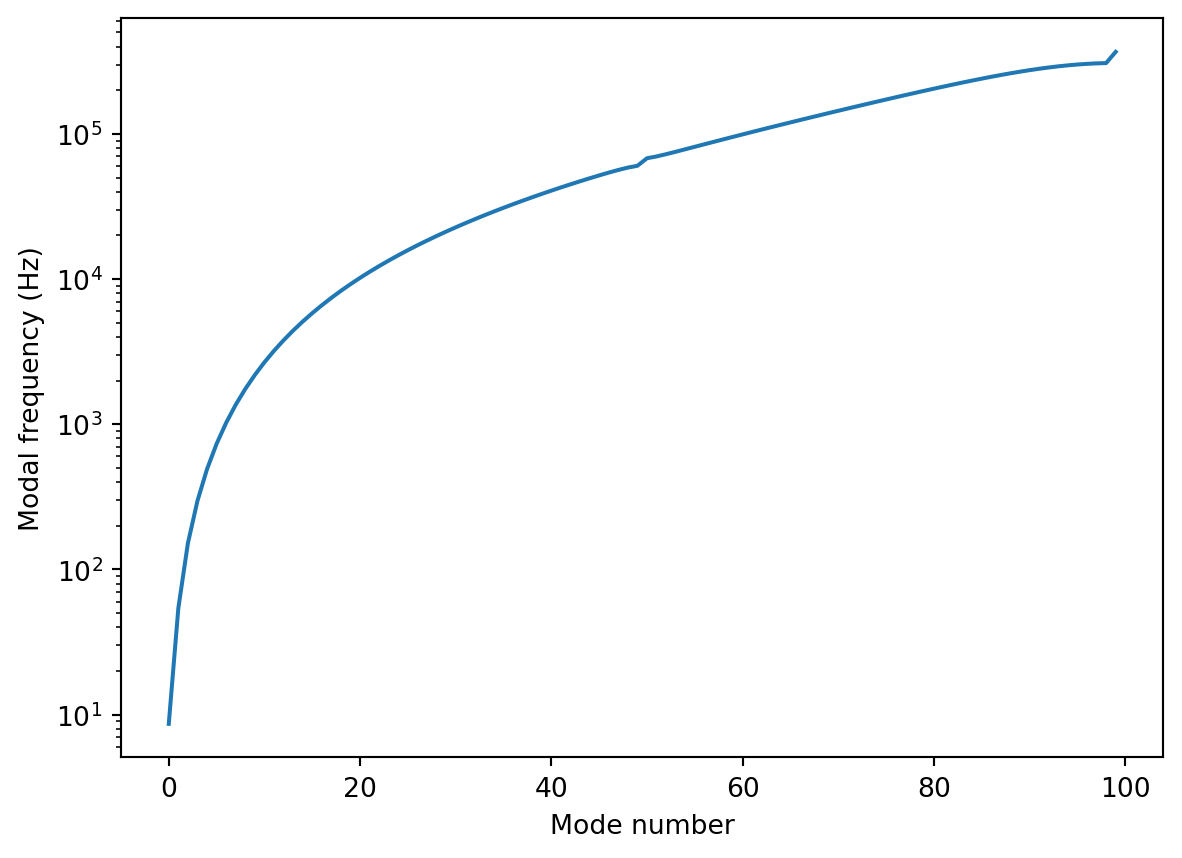
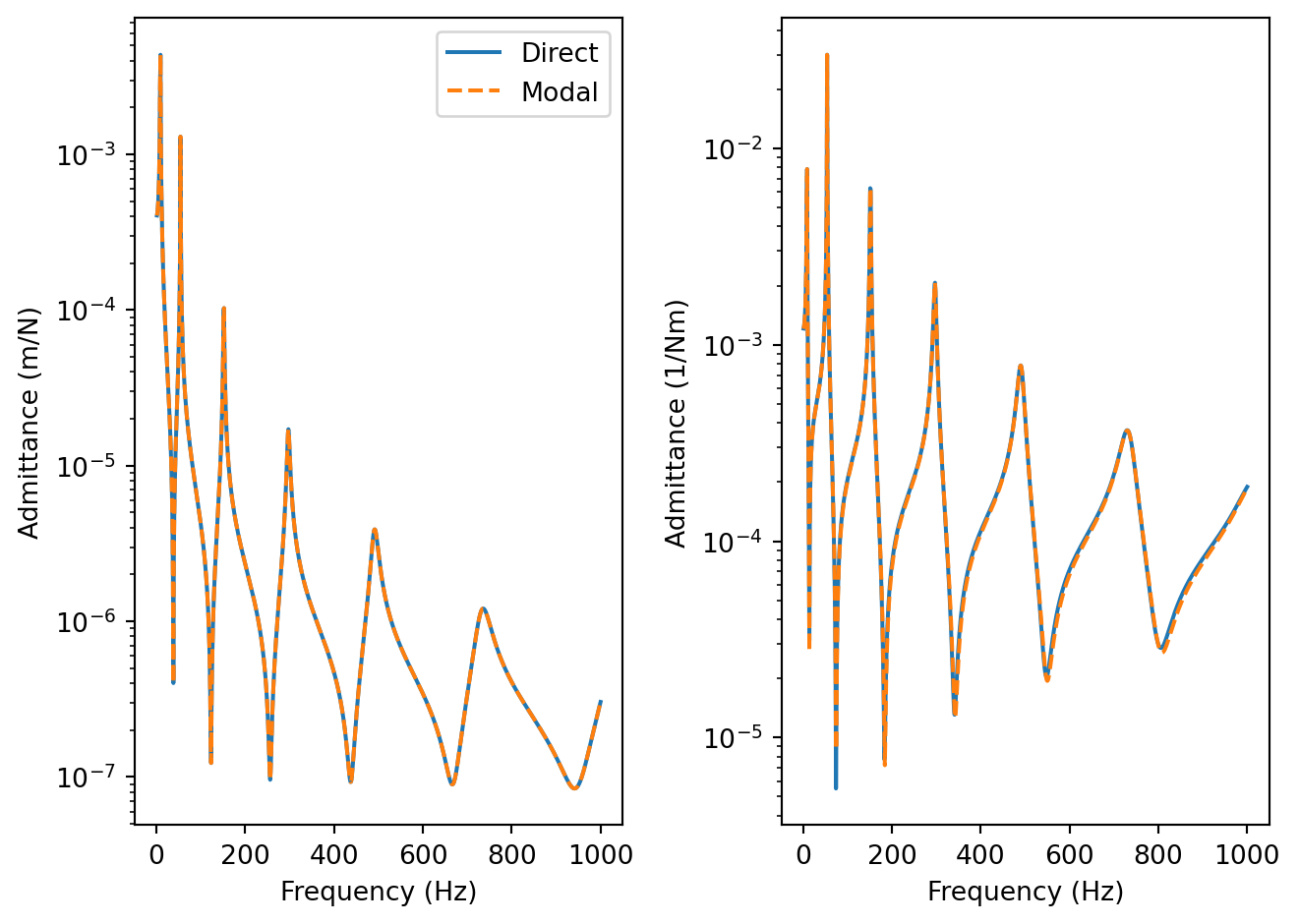
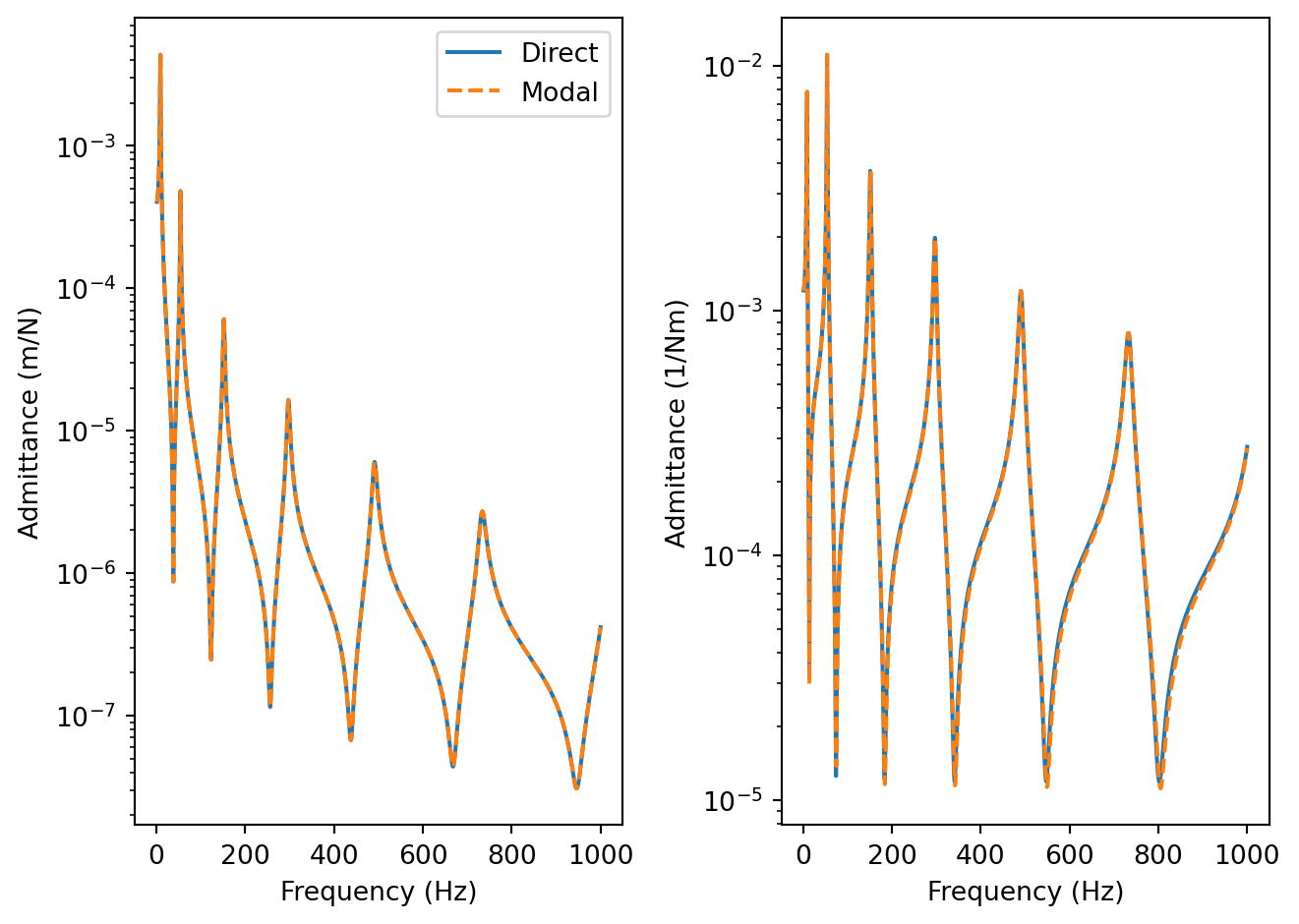
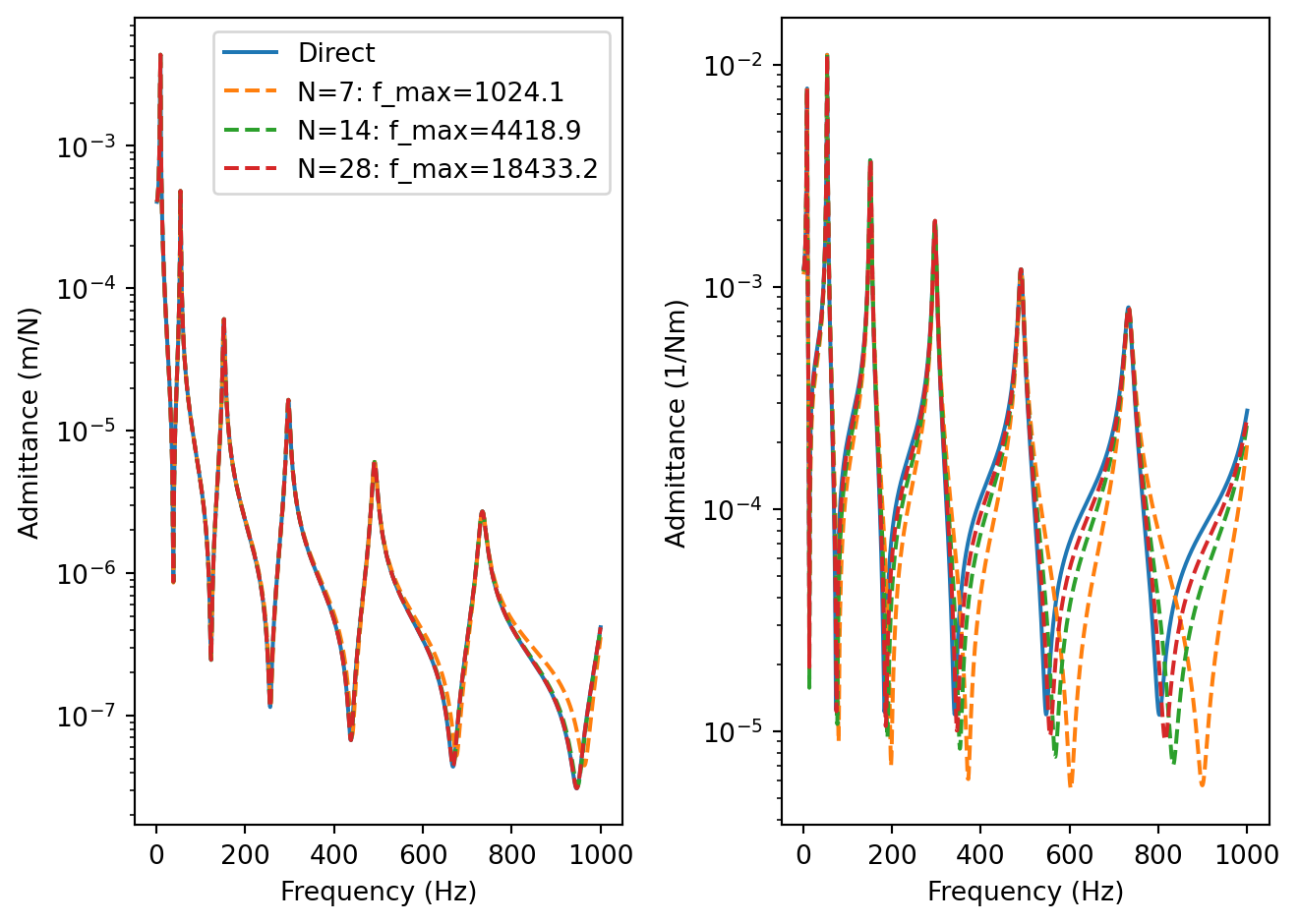
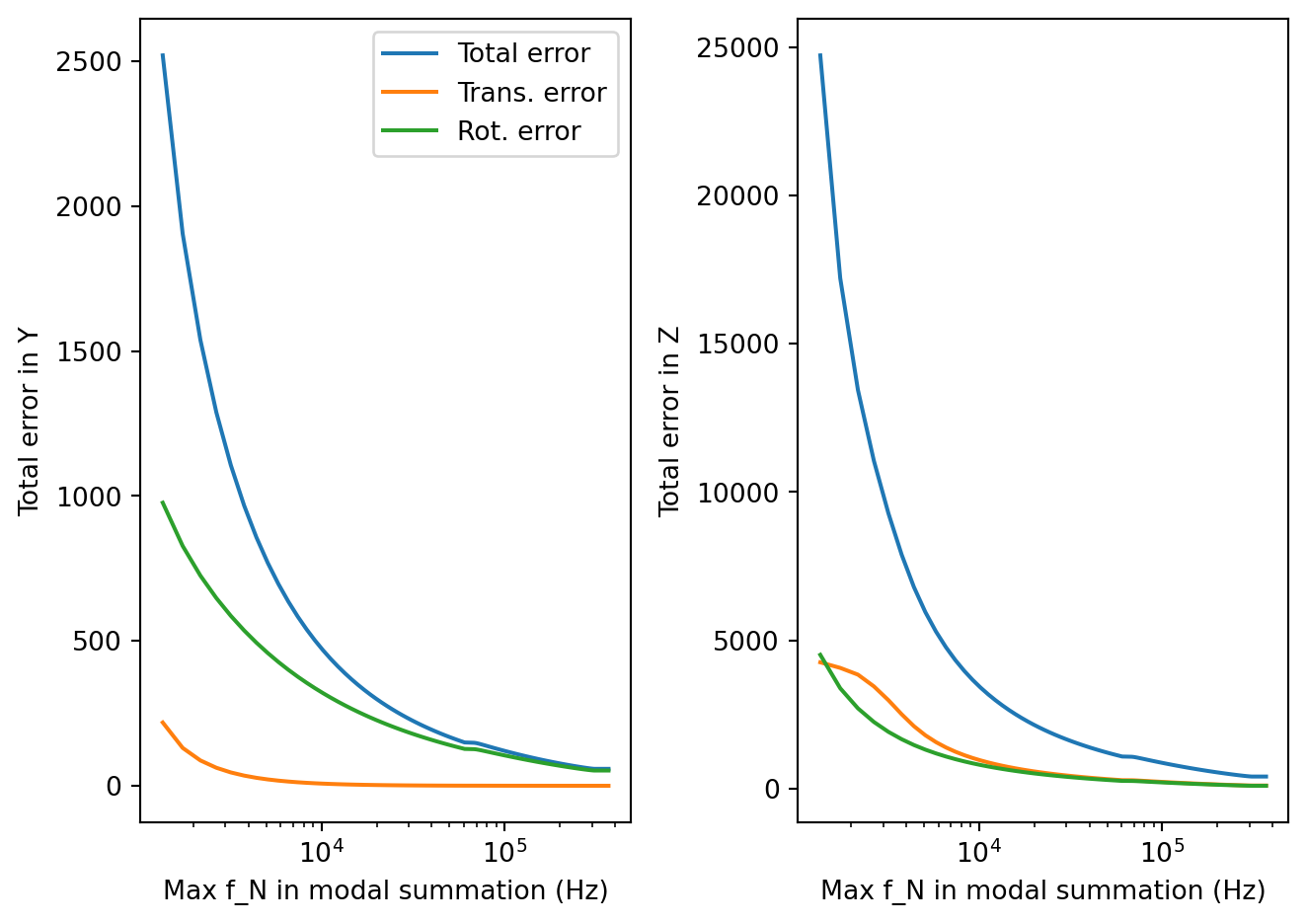
Code
import numpy as np
np.set_printoptions(linewidth=250)
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import scipy as sp
import sys as sys
f = np.linspace(0,100,1000) # Generate frequency array
ω = 2*np.pi*f # Convert to radians
# Define component masses and build matrices
m1, m2, m3, m4, m5 = 1, 2, 2, 1, 0.5
m6, m7, m8, m9, m10, m11 = 0.5, 2, 1, 3, 5,0.5
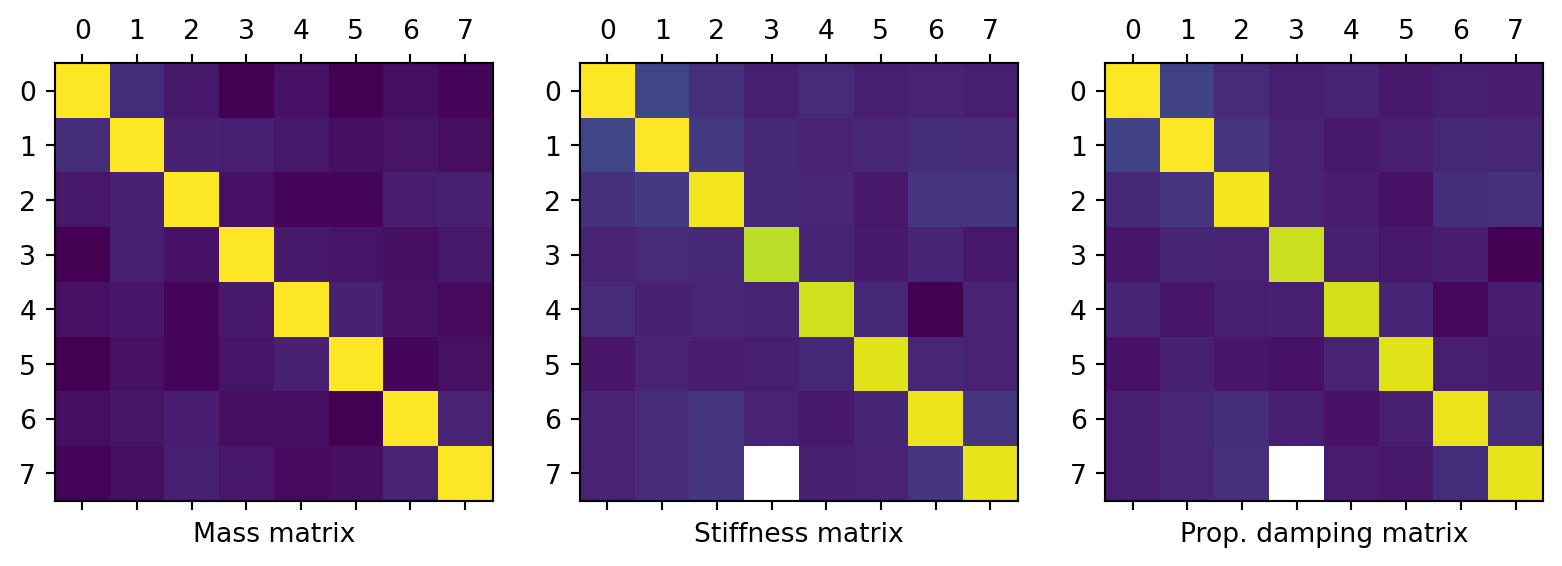
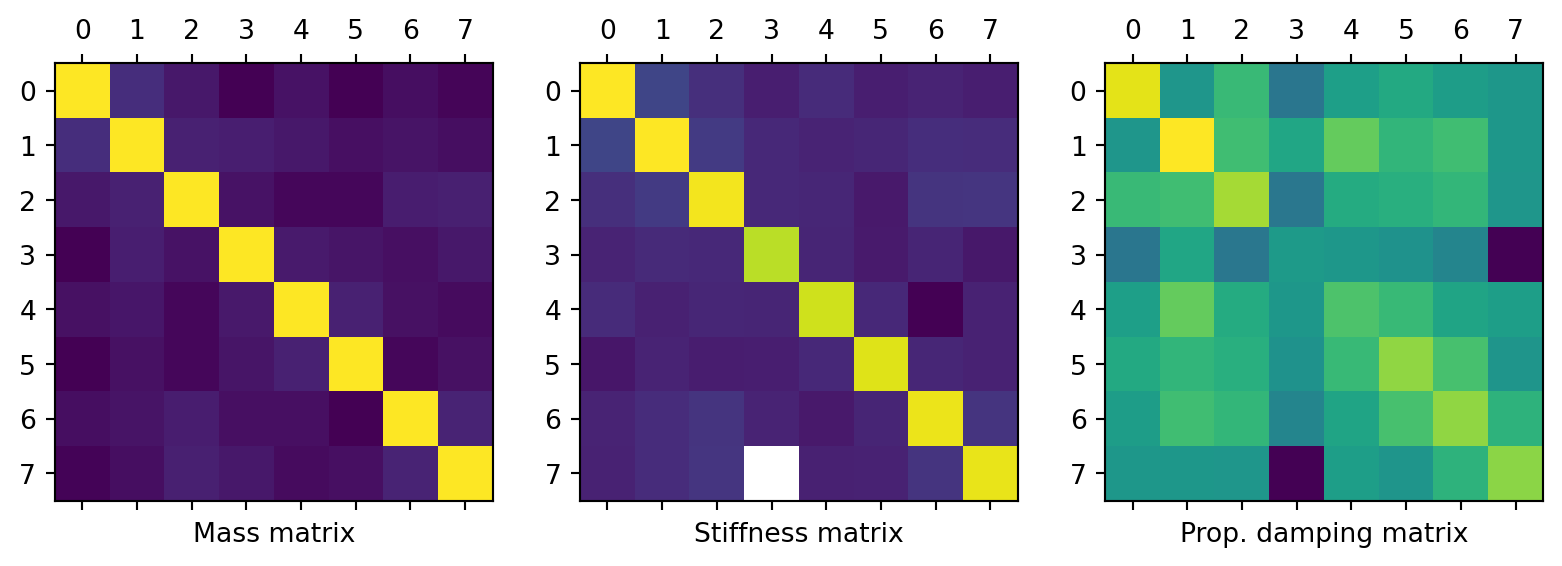
M_C = np.diag(np.array([m1,m2,m3+m6,m4+m7,m5+m8,m9,m10,m11])) # Coupled AB
# Define component stiffnesses and build matrices (complex stiffness -> structural damping)
η = 0.05 # Structural loss factor
k1, k2, k3, k4, k5 = 1, 1.5, 0.7, 1, 0.5
k6, k7, k8, k9, k10, k11 = 0.5, 2, 1, 0.2, 1, 0.5
K_C = np.array([[k1+k2+k5, -k2, 0, 0, -k5, 0, 0, 0],
[-k2, k2+k3+k4, -k3, -k4, 0, 0, 0, 0],
[0, -k3, k3+k6, 0, 0, -k6, 0, 0],
[0, -k4, 0, k4+k7, 0, 0, -k7, 0],
[-k5, 0, 0, 0, k5+k8, 0, -k8, 0],
[0, 0, -k6, 0, 0, k6+k9, 0, -k9],
[0, 0, 0, -k7, -k8, 0, k7+k8+k10, -k10],
[0, 0, 0, 0, 0, -k9, -k10, k9+k10+k11]])*1e5
print('Mass matrix of assembly (kg):\n' + str(M_C))
print('')
print('Stiffness matrix of assembly (m/N):\n' + str(K_C))
print('')Mass matrix of assembly (kg):
[[1. 0. 0. 0. 0. 0. 0. 0. ]
[0. 2. 0. 0. 0. 0. 0. 0. ]
[0. 0. 2.5 0. 0. 0. 0. 0. ]
[0. 0. 0. 3. 0. 0. 0. 0. ]
[0. 0. 0. 0. 1.5 0. 0. 0. ]
[0. 0. 0. 0. 0. 3. 0. 0. ]
[0. 0. 0. 0. 0. 0. 5. 0. ]
[0. 0. 0. 0. 0. 0. 0. 0.5]]
Stiffness matrix of assembly (m/N):
[[ 300000. -150000. 0. 0. -50000. 0. 0. 0.]
[-150000. 320000. -70000. -100000. 0. 0. 0. 0.]
[ 0. -70000. 120000. 0. 0. -50000. 0. 0.]
[ 0. -100000. 0. 300000. 0. 0. -200000. 0.]
[ -50000. 0. 0. 0. 150000. 0. -100000. 0.]
[ 0. 0. -50000. 0. 0. 70000. 0. -20000.]
[ 0. 0. 0. -200000. -100000. 0. 400000. -100000.]
[ 0. 0. 0. 0. 0. -20000. -100000. 170000.]]