Vibration isolators
On this page we intoduce the in situ method for isolator characterisation. Whilst alternative methods exist, including international standard series ISO 10846, we focus on the in situ method as: 1) we have found it to be the most convenient method in terms of implementation, 2) it provides reliable results over a braod frequency range, and 3) it has proven itself within the VAVP framework.
Isolator characterisation
If an isolator or resileint element is to be used within a VAVP, it must be charactersied independently in manner consistent with the component-based paradigm. The complete and independent characterisation of a coupling element is provided by its free-interface FRF matrix, \[ \mathbf{Y}_{I} = \left[\begin{array}{cc} \mathbf{Y}_{I{c_1c_1}} & \mathbf{Y}_{I{c_1c_2}} \\ \mathbf{Y}_{I{c_2c_1}} & \mathbf{Y}_{I{c_2c_2}} \end{array}\right] \] where \(c_1\) and \(c_2\) represent the DoFs at the two ends of the element, and the subscript \(I\) that the coupling element is in isolation.
Often when dealing with vibration isolators, or more presicely, vibration isolated systems, we talk of transmissibility as a means of characterisation. Whilst transmissibility provides a convenient means of assessing the performance of an isolation system, it is important to note that it is not an independent property of the isolator itself but includes properties of the isolated component. A change in the mass of this component will lead to a change in the transmissibility. Whats more, hwils the transmissibility is indeed a type of FRF (i.e. an input output relation), it is defined between two like quantities, for example force input to force output (or motion input to motion output). Hence, it does not contain sufficient information to allow for structural coupling, and is therefor of no use within the VAVP framework.
As mentioned on the previous page, for coupling elements free-interface FRFs are challenging to measure, and not necessarily representative. For this reason, a much greater emphasis has been placed on their so-called fixed-interface dynamics. Indeed, historically the preferred quantity to characterise a resilient element has been the dynamic transfer stiffness (recall that dynamic stiffness, like impedance and effective mass, has a kinematic constraint in its defintion), denoted \(\mathbf{D}_{I{ij}}\) (or \(\mathbf{D}_{I{ji}}\)), which describes the relation between an applied displacement at one side of the element to the resultant blocked force at the other, \[ \mathbf{\bar{f}}_{i} = \mathbf{D}_{Iij} \mathbf{x}_{j} {\big{|}_{\mathbf{x}_i=0, i\neq j}}. \] The term dynamic indicates that, in contrast to static stiffness which is constant, the dynamic stiffness is frequency-dependent and indeed for isolators, often displays significant variation with frequency. In addition, isolator properties may be sensitive to static pre-load, dynamic excitation level, temperature and relative humidity. These non-linearities make the complete characterisation of a resilient element a complicated and involved task. Nevertheless, for most practical situations (excluding extreme environmental conditions) a reasonable characterisation can be obtained by considering an element’s linear (small excitation) behaviour under an appropriate pre-load and at a given temperature.
Assuming a single point-like connection at each end (thus excluding distributed elements such as resilient matting), the point and transfer impedances of a coupling element are completely described by \(6\times 6\) matrices of the form, \[\label{} \mathbf{Z}_{I{c_ic_j}} = \left[\begin{array}{cccccc} Z_{I{x_ix_j}} & Z_{I{x_iy_j}} & Z_{I{x_iz_j}} & Z_{I{x_i\alpha_j}} & Z_{I{x_i\beta_j}} & Z_{I{x_i\gamma_j}} \\ Z_{I{y_ix_j}} & Z_{I{y_iy_j}} & Z_{I{y_iz_j}} & Z_{I{y_i\alpha_j}} & Z_{I{y_i\beta_j}} & Z_{I{y_i\gamma_j}} \\ Z_{I{z_ix_j}} & Z_{I{z_iy_j}} & Z_{I{z_iz_j}} & Z_{I{z_i\alpha_j}} & Z_{I{z_i\beta_j}} & Z_{I{z_i\gamma_j}} \\ Z_{I{\alpha_i x_j}} & Z_{I{\alpha_i y_j}} & Z_{I{\alpha_i z_j}} & Z_{I{\alpha_i\alpha_j}} & Z_{I{\alpha_i\beta_j}} & Z_{I{\alpha_i\gamma_j}} \\ Z_{I{\beta_i x_j}} & Z_{I{\beta_i y_j}} & Z_{I{\beta_i z_j}} & Z_{I{\beta_i\alpha_j}} & Z_{I{\beta_i\beta_j}} & Z_{I{\beta_i\gamma_j}}\\ Z_{I{\gamma_i x_j}} & Z_{I{\gamma_i y_j}} & Z_{I{\gamma_i z_j}} & Z_{I{\gamma_i\alpha_j}} & Z_{I{\gamma_i\beta_j}} & Z_{I{\gamma_i\gamma_j}} \end{array}\right], \] where, for example, \(Z_{I{z_i\beta_j}}\) represents the transfer impedance relating an applied angular velocity about the \({y}\) axes at interface \(j\), to the resultant translational blocked force in the \({z}\) direction at interface \(i\). The complete isolator impedance matrix \(\mathbf{Z}_{I}\) is thus \(12\times 12\).
With regards to characterisation methods for resilient elements, broadly speaking, they can be categorised as either experimental or model-based, with the former being further categorised as either direct or indirect. Direct methods involve the direct measurement of force for the transfer impedance, whereas with indirect methods these quantities are inferred from other, usually more easily measured quantities. Model-based methods typically involve establishing a numerical or analytical model that describes the underlying physics of the element, followed by a model updating procedure to determine the model inputs. Here, are focus is on experimental methods.
Blocking mass methods
Before introducing the in situ method of isolator characterisation it is worth breifly describing the more classical approaches described in ISO 10846. Both methods rely on the use of a blocking mass to physically enforce the kinematic constraint in the defintiion of transfer stiffness/impedance. The so-called direct method (ISO 10846-2) approximates the blocking force by installing a force transducer between the coupling element and the blocking mass. The in-direct method (ISO 10846-3) infers this force from the mass of the blocking mass \(m\), and its acceleration \(a\) using Newton’s 2nd law, \(F=ma\).
Though standardised, these blocking mass methods are not well suited to the needs of a VAVP. First of all, they are rather impractical. The blocking masses are typically many hundereds of kg making the expeirmental set-up quite substantial. Secondly, to charactrise an element in multiple DoFs (often required for a VAVP), multiple different test configurations are required. This makes the complete characterrisation of an element increidbly time consuming. Thirdly, the use of blocking mass tends to limit the frequency range of applicability. And fourthly, the blocking mass methods are only designed to provie transfer characteristics. The full characterisation of an element requires also a characterisation of the point dynamics are either end. All of these limitations are overcome by the in situ method described below.
In situ method (inverse substructuring)
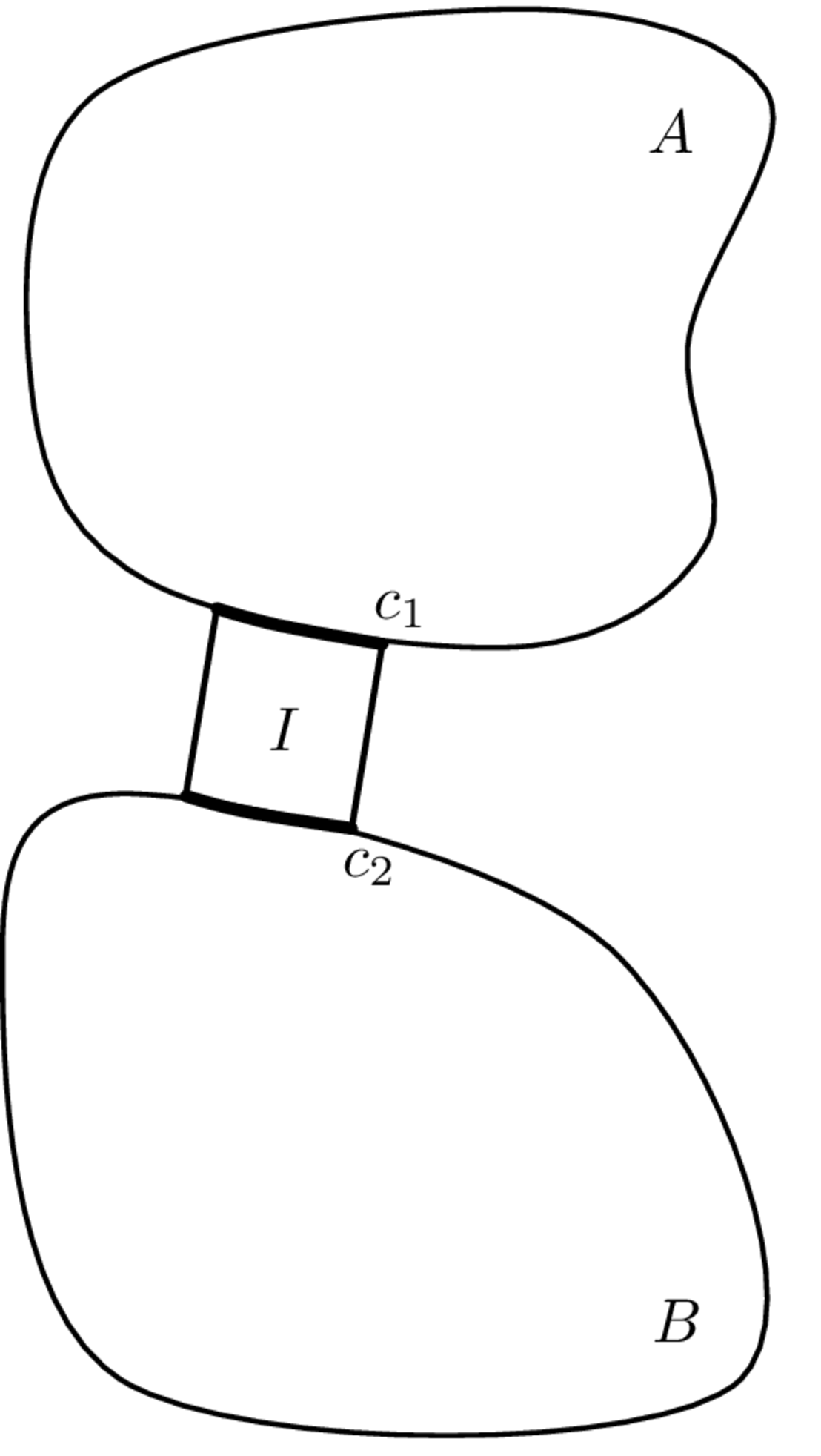
The blocking mass methods described above determine the transfer impedance elements \(Z_{ij}\) of a resilient element by physically constraining one end with a blocking mass. In-situ methods achieve these same constraints, instead, by mathematical means. As well as avoiding the need for a blocking mass this opens up the potential for characterising elements while in real installations which by definition provides realistic operating conditions such as pre-load.
The in-situ characterisation of a resilient element involves the extraction of invariant component properties from measurements made on a coupled assembly, i.e. with the element installed between two arbitrary components, \(A\) and \(B\) (Figure 1). To see how this is possible we construct the impedance matrix for an AIB assembly, i.e. an isolator \(I\) between substructures \(A\) and \(B\), noting that the impedance matrix of the assembly is given by the sum of those of the individual substructures (see Substructuring for more details on impedance coupling): \[ \mathbf{Z}_{Ccc} = \mathbf{Z}_{Acc} + \mathbf{Z}_{Icc} + \mathbf{Z}_{Bcc} \] or when written out in expanded form, \[ \left[ \begin{array}{cc} \mathbf{Z}_{Cc_1c_1} & \mathbf{Z}_{Cc_1c_2} \\ \mathbf{Z}_{Cc_2c_1} & \mathbf{Z}_{Cc_2c_2} \\ \end{array}\right] = \left[ \begin{array}{cc} \mathbf{Z}_{Ac_1c_1} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array}\right] + \left[ \begin{array}{cc} \mathbf{Z}_{Ic_1c_1} & \mathbf{Z}_{Ic_1c_2} \\ \mathbf{Z}_{Ic_2c_1} & \mathbf{Z}_{Ic_2c_2} \\ \end{array}\right] + \left[\begin{array}{cc} \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{Z}_{Bc_2c_2} \end{array}\right] \tag{1}\] where as usual \(C\) represents assembly properties and \(A\), \(B\) and \(I\) those of the substructures. Rewriting gives, \[ \mathbf{Z}_{Ccc} = \begin{bmatrix} \mathbf{Z}_{Ac_1c_1} + \mathbf{Z}_{Ic_1c_1} & \mathbf{Z}_{Ic_1c_2} \\ \mathbf{Z}_{Ic_2c_1} & \mathbf{Z}_{Bc_2c_2} + \mathbf{Z}_{Ic_2c_2} \end{bmatrix} = \mathbf{Y}_{Ccc}^{-1} \tag{2}\] where it is recalled that the impedance matrix \(\mathbf{Z}_{Ccc}\) is simply the inverse of the FRF matrix \(\mathbf{Y}_{Ccc}\).
The remarkable conclusion from Equation 2 is that the off-diagonal elements of the assembly’s impedance matrix, obtained by inverting the measurable coupled FRF, are identically equal to those of the isolator alone (\(\mathbf{Z}_{Ic_2c_1}\) or \(\mathbf{Z}_{Ic_1c_2}\)) and completely independent of the connected substructures \(A\) and \(B\).
This important result can be explained from the definition of impedance: for the transfer impedance \(\mathbf{Z}_{Ic_2c_1}\), the blocking force constraint at \(c_2\) in the definition of impedance essentially removes the dynamic influence of component \(B\), whilst at the same time, the velocity at \(c_1\) is applied irrespective of the dynamics of \(A\), and so neither \(A\) or \(B\) contribute to \(\mathbf{Z}_{Ic_2c_1}\). Obviously, a similar argument applies in the other direction.
An important consequence of Equation 2 is that it provides a means of independently characterising a coupling element in situ, i.e. whilst installed within an arbitrary assembly. Furthermore, recalling that the interface DoFs \(c_1\) and \(c_2\) are assumed to include all 6 pont-like DoFs (i.e. three translations and three rotations), the transfer impedance \(\mathbf{Z}_{Ic_1c_2}\), by definition, constrains all the DoFs included in \(\mathbf{Y}_C\). This enables the simultaneous characterisation of both in-plane and rotational transfer impedance terms. In essence, the act of numerically inverting the FRF matrix \(\mathbf{Y}_C\) constrains all the DoFs that are included within it. If a particular DoF is omitted, it will not be constrained by the matrix inversion, and so the resulting impedance terms will not be subject to the correct set of constraints.
In summary, the in-situ characterisation of a resilient element is performed as follows:
- Install the element within a representative assembly. This might be a bespoke test rig that applies an appropriate pre-load, or an actual installation.
- Instrument the interfaces above and below the isolator such that the DoFs of interest can be resolved.
- Measure the coupled mobility by exciting above and below the element, and recording their simultaneous responses.
- Apply appropriate interface transformation to obtain \(\mathbf{Y}_C\) and invert numerically.
- Extract the off-diagonal transfer impedance \(\mathbf{Z}_{Ic_1c_2}\) or \(\mathbf{Z}_{Ic_2c_1}\), which independently characterises the element \(I\).
It is important to note that the in-situ method, like the blocking mass methods described above, provides an estimate of only the transfer impedance, and that a complete characterisation also requires the point impedance matrices \(\mathbf{Z}_{Ic_1c_1}\) and \(\mathbf{Z}_{Ic_2c_2}\) to be known. As shown in Equation 2, the point impedance determined by the above procedure is that of the coupled \(AI\) or \(IB\) assemblies so a full characterisation cannot be obtained from in situ measurements alone. Methods to estimate the missing point impedances are presented below.
Force conservation
If the coupling element can be assumed massless, i.e. it behaves like an ideal spring-damper, the interface forces (\(\mathbf{g}\)) acting on the element are conserved across its length such that, \[ \mathbf{g}_{c_1} = -\mathbf{g}_{c_2}. \] Based on this assumption, the transfer impedance and point impedance are related as, \[ \mathbf{Z}_{Ic_1c_1} \approx -\mathbf{Z}_{Ic_1c_2}. \] The entire coupling element impedance matrix can then be approximated by, \[ \left[\begin{array}{c c} \mathbf{Z}_{Ic_1c_1} & \mathbf{Z}_{Ic_1c_2} \\ \mathbf{Z}_{Ic_2c_1} & \mathbf{Z}_{Ic_2c_2} \\ \end{array}\right] \approx \left[\begin{array}{c c} -\mathbf{Z}_{Ic_1c_2} & \phantom{-}\mathbf{Z}_{Ic_1c_2} \\ \phantom{-}\mathbf{Z}_{Ic_2c_1} & -\mathbf{Z}_{Ic_2c_1} \\ \end{array}\right]. \] Note that the above approximation is only valid where the coupling element satisfies the assumption of force conservation. This is largely the case for conventional vibration isolators at low frequencies when considering translational motions.
Decoupling
In cases where the force conservation does not apply, for example at higher frequencies where internal isolator resonances or DoF cross-coupling become significant, then the point impedance cannot be inferred from the transfer impedance. However, if the free interface FRF matrices of components \(A\) and \(B\) are known, then a decoupling procedure can be used, essentially by solving Equation 1 for the unknown isolator point FRFs, \[\label{isoDecouple} \left[\begin{array}{c c} \mathbf{Z}_{Ic_1c_1} & \mathbf{Z}_{Ic_1c_2} \\ \mathbf{Z}_{Ic_2c_1} & \mathbf{Z}_{Ic_2c_2} \\ \end{array}\right] = \left[\begin{array}{c c} \mathbf{Y}_{Cc_1c_1} & \mathbf{Y}_{Cc_1c_2} \\ \mathbf{Y}_{Cc_2c_1} & \mathbf{Y}_{Cc_2c_2} \\ \end{array}\right]^{\mathbf{-1}}- \left[\begin{array}{c c} \mathbf{Y}_{Ac_1c_1} & \mathbf{0} \\ \mathbf{0} & \mathbf{Y}_{Bc_2c_2} \\ \end{array}\right]^{-1} \] where we have substituted the impedance matrices for \(C\), \(A\) and \(B\) for the inverse of the respective FRFs.
In practice, this method is most likely to be applied using specially designed components for \(A\) and \(B\). Note that interface transformations may similarly be incorporated within this decoupling procedure (applied to both coupled \(C\) and uncoupled \(A\) and \(B\) measurements) to obtain the translation/rotational point impedance matrices.
What next?
We now have a means of charactrising the passive properties of all component types; source and receviers by approximating a free boundary condition and measuring directly their free-interface FRFs; and resilient couplings by installing them within an assembly, characterising their transfer impedance by the in situ method, and then their point impedance by either force conservation or decoupling. We now have everything we need to virtually assemble our components and build a model of a coupled assembly. This assembly process is called substructuring and is discussed on the next page!